Расчёт вероятности ошибки для BPSK
Введение
Моя сеть приёма сигналов со спутников r2cloud постепенно растёт. Однако уровень приёма оставляет желать лучшего. Несмотря на то, что на спектограмме виден сигнал, демодулятор не может восстановить его. В попытках найти проблему, я понял, что мне не хватает фундаментальных знаний по теории обработки сигналов и некоторой математики. Дело в том, что в интернете зачастую выкладываются демодуляторы без обоснования их работы. Меня это не устраивает, потому что нужны метрики по которым я буду понимать насколько один алгоритм эффективнее другого. И стал ли новый код лучше, если я добавлю какой-нибудь другой блок в обработку.
Всё это привело меня к \( E_b / N_0 \). Эта метрика показывает отношение энергии сигнала, приходящейся на 1 бит принимаемого сообщения (\( E_b \)), к энергетической спектральной плотности шума (\( N_0 \)). Почему она так важна? Дело в том, что она не зависит от способа модуляции сигнала и пропускной способности канала. Из-за этого её можно использовать, чтобы сравнивать различные модуляции между собой. Обычно строят график отношения \( E_b / N_0 \) к вероятности ошибки (BER). Вот пример графика сравнения BPSK/QPSK/8-PSK/16-PSK:
Что из этого графика можно понять?
- Если увеличивать энергию передаваемого бита, то уменьшается вероятность возникновения ошибки.
- В BPSK/QPSK ошибка возникает значительно реже, чем в 8-PSK и 16-PSK при одинаковых значениях энергии передаваемого бита.
- График, например, читается следующим образом: при \( E_b / N_0 \) равным 4 децибелла и BPSK модуляции можно получить 1 ошибочный бит на каждые 100 полученных.
Мне же график прежде всего нужен:
- Сравнивать теоретические значения с практической реализацией демодулятора. Прямо сейчас я точно знаю, что различия есть из-за ограниченной точности АЦП. Дело в том, что rtl-sdr имеет разрешающую способность 8 бит. А в теории числа могут быть бесконечной точности. Именно эта разница и должна давать ошибку.
- Анализировать улучшится ли демодулятор, если добавить какой-то определённый блок. Как минимум я хочу попробовать различные алгоритмы получения несущего сигнала и компенсации многолучевого распространения.
Ну и для того, чтобы понять математику, я решил проделать выводы сам. Ниже я буду рассчитывать вероятности ошибки для BPSK (см. синий график выше). Вдохновение я черпал у dsplog плюс добавлял свои мысли.
Дано
Прежде всего необходимо описать физику процесса. Схема процесса показана ниже:
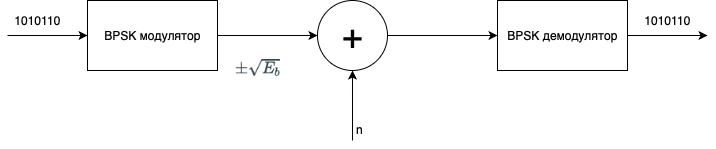
- Изначальное сообщение кодируется в аналоговый сигнал. “1” кодируется в \(+\sqrt{E_b}\), “0” кодируется в \(-\sqrt{E_b}\). Почему именно как корень из \(E_b\)? Не знаю. Это единственное место, где я не разобрался.
- После этого сигнал складывается с аддитивным белым гауссовским шумом.
- Далее сигнал демодулируется.
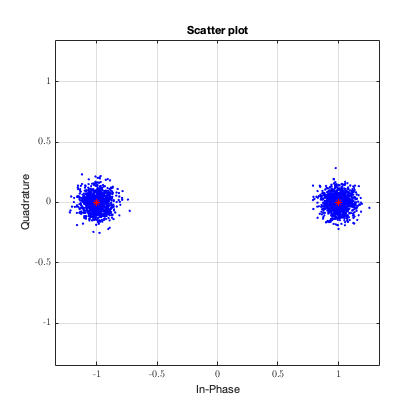
Модулированный BPSK сигнал выглядит следующим образом:
Красными точками обозначается сигнал без шума. Синими - сигнал с добавлением белого гауссовского шума. Как демодулируется этот сигнал? Все точки, которые больше “0” становятся “1”, а те, что меньше “0” становятся “0”. На рисунке выше все синие точки достаточно далеко от “0”, поэтому информацию можно однозначно восстановить. Но что если шум будет сильнее?
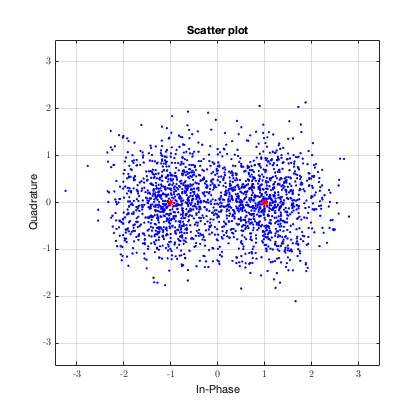
Тут уже не всё так однозначно. Видно, что некоторые точки закодированные как “1” на самом деле оказались меньше “0”. И если бы я попытался их демодулировать, то получил бы неправильную информацию.
Решение
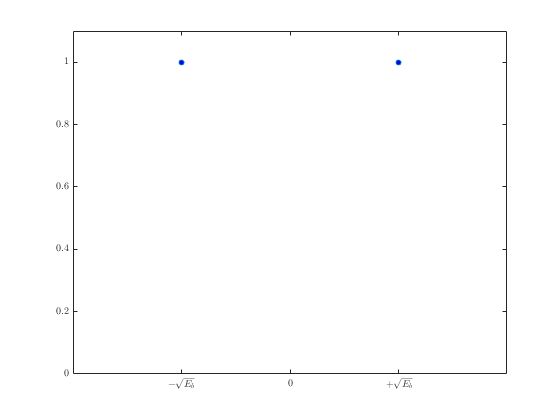
Теперь, когда стало понятно влияние шума на результат демодуляции, можно переходить к графику зависимости вероятности от энергии сигнала. Этот график поможет посчитать вероятность ошибок для различных входных значений. Для начала возьмём сигнал без шума. Вероятность получения “0” или “1” всегда 1.
Частота получения ошибочных битов (Bit error rate) будет 0. Т.е. 0 ошибочных битов на бесконечное количество принятых. В случае наличия гауссовского шума, вероятность получения определяется гауссовской функцией вероятности:
Гауссовский шум определяется следующей формулой:
$$ p(x) = \dfrac{1}{\sqrt{2\pi\sigma^2}}e^\dfrac{-(x-\mu)^2}{2\sigma^2} $$
Где:
- \(\mu=0\),
- \(\sigma^2=N_0/2\)
При передаче “1” \(\mu=+\sqrt{E_b}\), при “0” \(\mu=-\sqrt{E_b}\). Подставляя это в формулу:
$$ \begin{align} P(x|s_0)=\dfrac{1}{\sqrt{\pi N_0}}e^\dfrac{-(x+\sqrt{E_b})^2}{N_0} \newline P(x|s_1)=\dfrac{1}{\sqrt{\pi N_0}}e^\dfrac{-(x-\sqrt{E_b})^2}{N_0} \end{align} $$
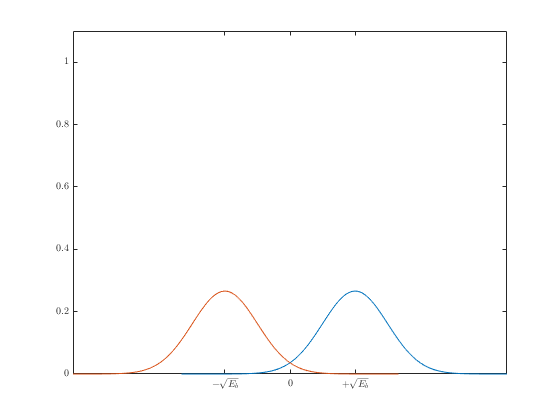
Теперь самое интересное.
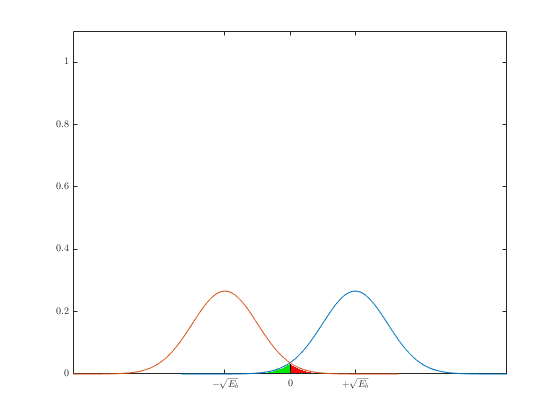
На этом рисунке показаны области возникновения ошибки. Зелёная область - это место, где возникает ошибка при передаче “1”, красная - при передаче “0”. Общую вероятность ошибки можно записать с помощью формулы полной вероятности:
$$ P(error)=\dfrac{1}{2}P(error|s_0) + \dfrac{1}{2}P(error|s_1) $$
После этого необходимо найти каждую из вероятностей:
$$ \begin{align} P(error|s_0) = \int_{0}^{\infty}P(x|s_0)dx = \dfrac{1}{\sqrt{\pi N_0}}\int_{0}^{\infty}e^\dfrac{-(x+\sqrt{E_b})^2}{N_0}dx \newline P(error|s_1) = \int_{-\infty}^{0}P(x|s_1)dx = \dfrac{1}{\sqrt{\pi N_0}}\int_{-\infty}^{0}e^\dfrac{-(x-\sqrt{E_b})^2}{N_0}dx \end{align} $$
Обычно вероятность ошибки записывают с помощью функции ошибок:
$$ erfc(x)=\dfrac{2}{\sqrt\pi}\int_{0}^{x}e^{-t^2}dt $$
Для этого необходимо сделать следующее:
$$ z=\dfrac{y+\sqrt{E_b}}{\sqrt{N_0}} => z\sqrt{N_0} = y + \sqrt{E_b} $$
Заменить пределы интегрирования:
$$ \begin{align} y=0 => z = \dfrac{\sqrt{E_b}}{\sqrt{N_0}} \newline y=\infty => z = \infty \end{align} $$
Получившаяся ошибка записывается как:
$$ \begin{align} P(error|s_0)=\dfrac{1}{\sqrt{\pi N_0}}\int_\limits{\sqrt{\dfrac{E_b}{N_0}}}^{\infty}e^{-z^2}\sqrt{N_0}dz =\dfrac{1}{\sqrt{\pi}}\int_\limits{\sqrt{\dfrac{E_b}{N_0}}}^{\infty}e^{-z^2}dz =\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}}) \end{align} $$
Аналогично можно найти ошибку при передаче “1”:
$$ \begin{align} P(error|s_1)=1-P(s_1)=1-\dfrac{1}{2}erfc(-\sqrt{\dfrac{E_b}{N_0}}) \end{align} $$
Можно воспользоваться свойством функции ошибок:
$$ \begin{align} erfc(-x)=2-erfc(x) => P(error|s_1) = \dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}}) \end{align} $$
Если подставить в формулу полной вероятности:
$$ P(error)=\dfrac{1}{2}(\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}})) + \dfrac{1}{2}(\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}}))=\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}}) $$
Ответ
Получившийся график: