Геокодирование спутниковых снимков: опорные точки
Начало
В прошлом посте я описал основные шаги, необходимые для геокодирования изображения. Здесь же, я хочу более подробно описать алгоритм получения опорных точек. Опорная точка - это отображение координат пиксела (X, Y) на географические координаты (широта, долгота).
Зная список опорных точек, можно растянуть изображение по ширине и высоте так, чтобы оно совпало с картой. Их, например, можно задать вручную в любой ГИС. Обычно выбирают береговые линии с характерными полуостровами:

Мне же такой способ не подходит, так как я хочу делать это в автоматическом режиме. Это более сложный способ, так как требуется смоделировать поведение спутника в каждый момент времени. А для этого нужно вычислить:
- положение спутника
- положение камеры относительно спутника
- параметры камеры (фокусное расстояние, пространственное разрешение и пр.)
Далее я постараюсь рассчитать каждый из этих параметров и посчитать на их основе опорные точки.
Положение спутника
Положение спутника можно получить двумя способами:
- На основе телеметрии, которую передаёт сам спутник
- На основе SGP4 модели
Несмотря на то, что первый способ более точный, Метеор-М2 не передаёт эту информацию. Но это не беда. Можно рассчитать чуть менее точное положение на основе модели SGP4. Для этого нужно знать:
- TLE
- текущее время
TLE
TLE - это двухстрочный формат данных, представляющий собой набор элементов орбиты для спутника Земли. Взять актуальные параметры можно с сайта www.celestrak.com. Например, в данный момент TLE для Метеор-М2 такие:
METEOR-M 2
1 40069U 14037A 20109.60817406 -.00000042 00000-0 -58409-8 0 9990
2 40069 98.5096 149.3859 0006903 94.0019 266.1946 14.20671606299713
Текущее время
Время - очень важный параметр, который нужно знать для каждой строчки изображения. Его можно получить двумя способами:
- На основе информации со спутника
- Рассчитать на станции приёма
К счастью, Метеор-М2 передаёт время формирования изображения в каждом пакете. В протоколе LRPT для этого существует вторичный заголовок, в котором может содержаться актуальное время:

Метеор-М2 передаёт в поле “мс суток” количество миллисекунд, прошедших с начала дня по московскому времени.
Расчёт положения
На основе этих данных можно посчитать положение спутника. Для этого я использую библиотеку orekit:
String line1 = "1 40069U 14037A 20109.60817406 -.00000042 00000-0 -58409-8 0 9990";
String line2 = "2 40069 98.5096 149.3859 0006903 94.0019 266.1946 14.20671606299713";
TLEPropagator tlePropagator = TLEPropagator.selectExtrapolator(new TLE(line1, line2));
AbsoluteDate date = new AbsoluteDate("2020-04-11T05:36:00.899994", TimeScalesFactory.getUTC());
PVCoordinates pv = tlePropagator.getPVCoordinates(date);
Здесь для примера я взял расчёт положения для времени 2020-04-11 05:36. Таким же образом можно найти положение для любой даты. Единственное, что нужно учитывать - это устаревание TLE. Посчитать траекторию спутника на длительном отрезке времени достаточно сложно и ресурсоёмко. Именно поэтому авторы SGP4 выбрали простые расчёты и периодическую коррекцию на основе визуальных наблюдений.
Если рассчитать положение спутника с 2020-04-11 05:36 по 2020-04-11 05:46 и наложить полученные координаты на Яндекс карты, то получится вот такая симпатичная картинка:
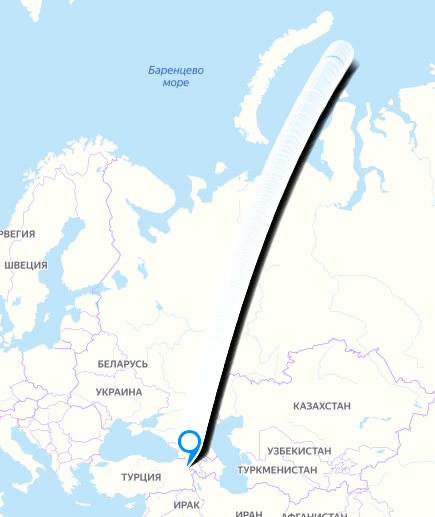
К слову, использование Яндекс карт оказалось очень удобным способом отладки.
Положение камеры относительно спутника
Следующим шагом необходимо понять направление камеры. Для этого необходимо вычислить кватернионы самого спутника. Согласно документации, камера спутника смотрит точно в надир. То есть, спутник равномерно вращается вокруг своей оси и при этом угол напрямую зависит от положения относительно Земли. Всё это можно смоделировать с помощью orekit:
String line1 = "1 40069U 14037A 20109.60817406 -.00000042 00000-0 -58409-8 0 9990";
String line2 = "2 40069 98.5096 149.3859 0006903 94.0019 266.1946 14.20671606299713";
TLEPropagator tlePropagator = TLEPropagator.selectExtrapolator(new TLE(line1, line2));
Frame eme2000 = FramesFactory.getEME2000();
Frame earthFrame = FramesFactory.getITRF(IERSConventions.IERS_2010, true);
OneAxisEllipsoid earth = new OneAxisEllipsoid(Constants.WGS84_EARTH_EQUATORIAL_RADIUS, Constants.WGS84_EARTH_FLATTENING, earthFrame);
BodyCenterPointing earthCenterAttitudeLaw = new BodyCenterPointing(eme2000, earth);
AbsoluteDate date = new AbsoluteDate("2020-04-11T05:36:00.899994", TimeScalesFactory.getUTC());
Attitude attitude = earthCenterAttitudeLaw.getAttitude(tlePropagator, date, eme2000);
Основная идея заключается в том, чтобы определить угол между базисными векторами спутника и вектором, соединяющим центр спутника и центр Земли. Конечно, для более точного позиционирования нужно использовать гравитационный центр Земли. А для этого использовать гравитационные карты Земли. К счастью, в случае Метеор-М2 и камеры MСУ-МР, такой точности не требуется.
Параметры камеры
Самый сложный шаг заключается в моделировании камеры МСУ-МР. Дело в том, что в интернете почти нет её параметров. Я почти разуверился в том, что это вообще возможно найти, однако мне удалось раскопать научную статью “МЕТОДИКИ ОПРЕДЕЛЕНИЯ ВЕЛИЧИНЫ ПРОЕКЦИИ ПИКСЕЛЯ СЪЁМОЧНЫХ СИСТЕМ МСУ-МР И КМСС НА МЕСТНОСТЬ”. В ней вскользь упоминаются параметры:
- количество точек N=1568
- общий угол обзора Θ = 110,5°
- фокусное расстояние. Зависит от типа канала:
- f=150мм,w=0,2 мм для каналов 1,2
- f=150мм,w=0,18мм для канала 3
- f=40мм, w=0,05мм для каналов 4,6
Схематично геометрия съёмки выглядит следующим образом:
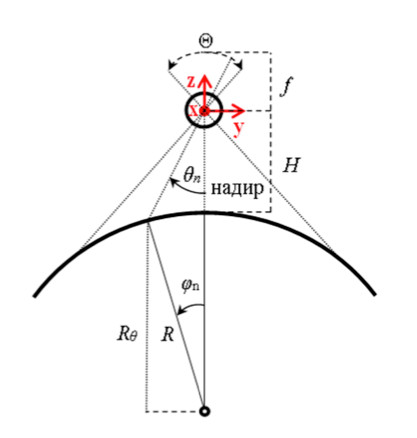
Для модели расчёта опорных точек мне нужно рассчитать вектора исходящие из камеры и направленные на поверхность. Если принять угол Θn = Θ * n / N, то вектора можно рассчитать следующим образом:
double width = 1568;
double delta = FastMath.toRadians(110.5) / width;
for (int i = 0; i < width; i++) {
SinCos sc = FastMath.sinCos((i - width / 2) * delta);
Vector3D curVector = new Vector3D(0.0, sc.sin(), sc.cos());
}
Построение опорных точек
На основе полученных параметров можно рассчитать опорные точки. Для этого надо вспомнить школьный курс неевклидовой геометрии и рассчитать проекции на сферу. Или можно взять готовую библиотеку Rugged. В ней описана достаточно сложная модель получения опорных точек. Она учитывает скорость света и относительную скорость спутника относительно Земли, модель рефракции атмосферы. Также можно, например, загрузить карту высот и получить более точные координаты.
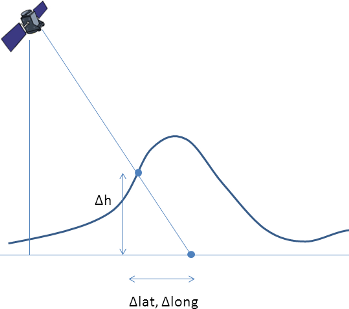
Для МСУ-МР такая точность не нужна, но это может быть полезно для других типов камер и спутников.
Центральным классом модели является Rugged. Его можно создать следующим способом:
LOSBuilder losBuilder = new LOSBuilder(rawDirs);
TimeDependentLOS lineOfSight = losBuilder.build();
MeteorLineDatation lineDatation = new MeteorLineDatation(image, startOfTheDay.getTime());
LineSensor lineSensor = new LineSensor("MSU_MR", lineDatation, Vector3D.ZERO, lineOfSight);
Rugged rugged = new RuggedBuilder().
// do not use Digital Elevation Model
setAlgorithm(AlgorithmId.IGNORE_DEM_USE_ELLIPSOID).
setEllipsoid(EllipsoidId.WGS84, BodyRotatingFrameId.ITRF).
// calculate 10 minute pass
setTimeSpan(absDate, absDate.shiftedBy(60 * 10), 0.01, 8 / lineSensor.getRate(0)).
setTrajectory(InertialFrameId.EME2000,
satellitePVList, 4, CartesianDerivativesFilter.USE_PV,
satelliteQList, 4, AngularDerivativesFilter.USE_R).
addLineSensor(lineSensor).
build();
Алгоритм следующий:
- создаётся
lineOfSightна основе параметров камеры - создаётся модель сенсора на основе
lineOfSightи, так называемого,LineDatation. Это объект, который позволяет на основе индекса строки получить дату и наоборот - для расчёта координат точек:
- используется проекция WGS84. Об этом будет чуть подробнее в следующей статье
- траектория спутника
satellitePVList - кватернионы спутника
satelliteQList
Как только объект создан, можно вычислить опорные точки:
int lineIndex = 0;
int pixelIndex = 0;
// position of sensor within spacecraft frame
Vector3D position = lineSensor.getPosition();
AbsoluteDate date = lineSensor.getDate(lineIndex);
// get line-of-sight
Vector3D los = lineSensor.getLOS(date, pixelIndex);
// calculate GCP
GeodeticPoint gcp = rugged.directLocation(date, position, los);
Результат
Для того чтобы проверить корректность модели, можно рассчитать опорные точки для каждого пиксела и нанести на карту. Например, неправильно рассчитанные квартернионы дают следующую картинку:
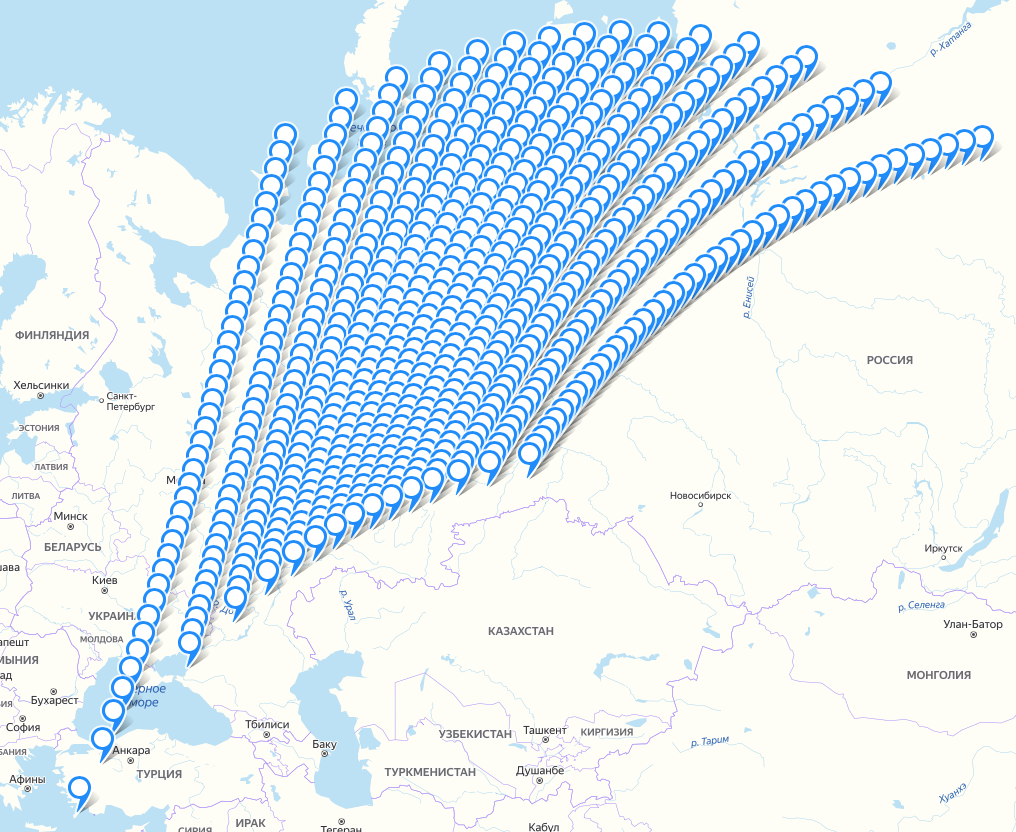
Судя по изображению, камера спутника сначала смотрит точно в надир, а потом начинает отклоняться вверх и влево.
Если все параметры заданы верно, то опорные точки должны выглядеть так:
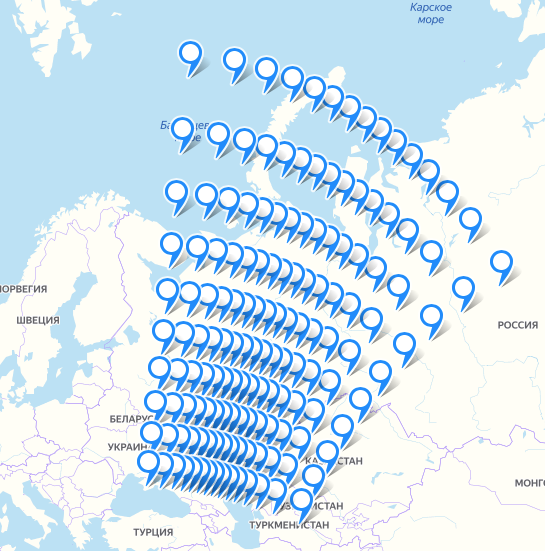
Здесь видно, что:
- Спутник летит под небольшим углом с севера на юг
- Расстояния между линиями увеличиваются с юга на север из-за проекции меркатора
- Расстояния между пикселами увеличиваются из центра к краям из-за широкоугольной камеры спутника
После того как получены опорные точки и они выглядят правдоподобно, можно переходить к следующему шагу: создание GeoTiff файла.
Геокодирование спутниковых снимков:
