Расчёт вероятности ошибки для FSK демодулятора

Введение

Прошёл почти год с того момента, когда я измерял BER для BPSK демодулятора. И вот пришло время измерить вероятность ошибки для FSK демодулятора. Поводом к такому исследованию послужило большое количество спутников, передающих частотно-модулированный сигнал. Мне хотелось прежде всего измерить текущие характеристики демодулятора, чтобы в последствии можно было его улучшать.

Описание теста

С прошлого раза я решил существенно поменять методологию. Раньше для подсчёта ошибок использовалось скремблирование. Все полученные нулевые биты делились на 6, из-за характеристик полинома скремблера и дифференциального кодирования. Такой способ работал хорошо для больших значений \( E_b / N_0 \). Однако, для маленьких значений, он не очень подходил. Например, на последнем графике видно, что демодулятор работал лучше теоретически возможного:

Более сложным, но и одновременно более точным способом подсчёта ошибок, будет использование корреляции сигналов. Для этого нужно найти корреляцию между входным потоком бит и выходящим из демодулятора. Прелесть этого подхода в следующем:

• строгое математическое доказательство.
• входящая последовательность бит может быть псевдослучайной последовательностью. Это очень сильно поможет демодулятору синхронизировать символы. А ещё это очень похоже на реальные данные.
• устойчивость к задержкам в демодуляторе. Некоторые блоки в демодуляторе могут задерживать входящий сигнал. Поэтому первый входящий бит не всегда равен первому исходящему биту.
• не требует специальных знаний об устройстве демодулятора. Например, при тестировании BPSK демодулятора я учитывал фазовую неоднозначность. Такой подход не сработал бы для тестирования FSK демодулятора.

Корреляция сигналов

Прежде, чем кодировать, нужно разобраться с матмоделью. Корреляция сигналов записывается как:

$$ (f \star g)[n]\ \triangleq \sum_{m=-\infty}^{\infty} \overline{f[m]} g[m+n] $$

Где,

\(f\) - входящий сигнал, \(g\) - выходной сигнал

Программировать бесконечный цикл не очень здорово, поэтому обычно используют теорему о свёртке и вычисляют преобразования Фурье:

$$ \mathcal{F}\left\{f \star g\right\} = \overline{\mathcal{F} \left\{f\right\}} \cdot \mathcal{F}\left\{g\right\} $$

Где,

\(\mathcal{F} \left\{f\right\}\) - преобразование Фурье входящего сигнала, \(\mathcal{F}\left\{g\right\}\) - преобразование Фурье выходного сигнала

После того как найдена корреляция сигналов, можно найти когерентность между ними:

$$ C_{fg}(n) = \frac{|\mathcal{F}\left\{f \star g\right\}|^2}{G_{ff}(n) G_{gg}(n)} $$

После осознания формул, алгоритм можно представить следующим образом:

• получение псевдослучайной последовательности “0” и “1”. Это будут исходные данные для передачи.
• преобразование данных в интервал “-1” и “1” и расчёт прямого преобразования Фурье.
• получение комплексного сопряжения \(\overline{\mathcal{F} \left\{f\right\}}\).
• передача исходных данных и получение выходного сигнала.
• преобразование выходного сигнала в интервал “-1” и “1” и расчёт прямого преобразования Фурье.
• получение корреляции \(\mathcal{F}\left\{f \star g\right\}\).
• обратное преобразование Фурье для того, чтобы получить значения кросс-спектральной плотности (cross-spectral density).
• получение ошибки из когерентности сигналов \(C_{fg}(n)\).

Этот метод выглядит значительно сложнее предыдущего. Тем не менее использование математики и формального доказательства даёт мне некоторую уверенность в результатах.

Результаты

Результатов мне пришлось ждать довольно долго. И не потому, что алгоритм работает достаточно долго. Нет. Несколько недель мне потребовалось для того, чтобы правильно настроить стенд. Например, нужно правильно отмасштабировать коэффициенты FFT преобразования и подобрать правильную скорость сэмплирования. Несмотря на то, что как такового сэмплирования нет, все блоки работает именно с коэффициентом сэмплирования и его нужно было правильно подобрать в разных местах.

В результате получились следующие графики:

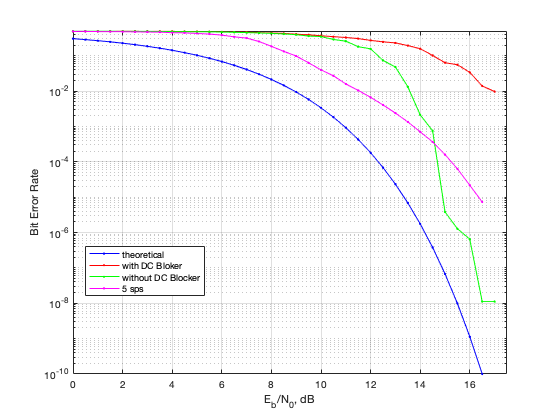
Как видно, я пробовал различные варианты, прежде чем получил более-менее сносный результат. Например, использование DC Blocker для блокирования DC сигнала, существенно ухудшало характеристики демодулятора.

Ещё одним открытием для меня стало то, что повышение количества сэмплов на символ (samples per symbol - sps) существенно улучшает качество приёма. На красном и зелёном графике я использовал sps=2, а на бордовом - sps=5.

Я попробовал заменить low pass filter на обычный прямоугольный, но результат получился не очень.

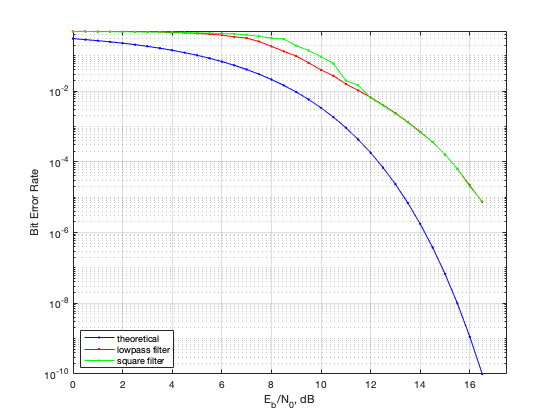
Ещё я померил как себя поведёт демодулятор с DC Blocker и без при sps=5. Результат чуть лучше, но я не готов его выкидывать, так как этот компонент помогает найти несущую частоту в реальных сигналах. Частота принимаемого сигнала может немного “плавать”. Иногда это происходит из-за приёмника, иногда на спутнике проблемы.

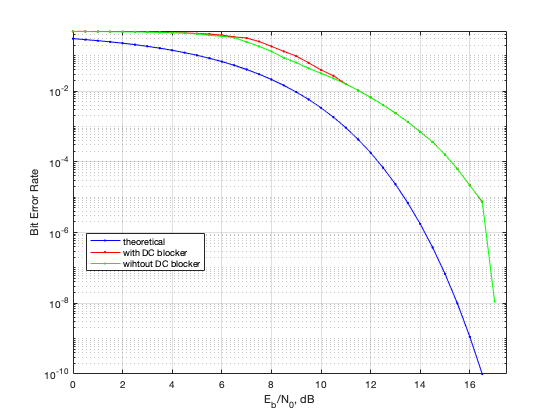
Что дальше?

После того как получена BER кривая, можно начинать улучшать демодулятор. Для начала я хочу попробовать заменить алгоритм синхронизации символов. Потом я попробую измерить скорость лока сигнала и скорость потери лока. Впереди, как обычно, много всего интересного и неизвестного.