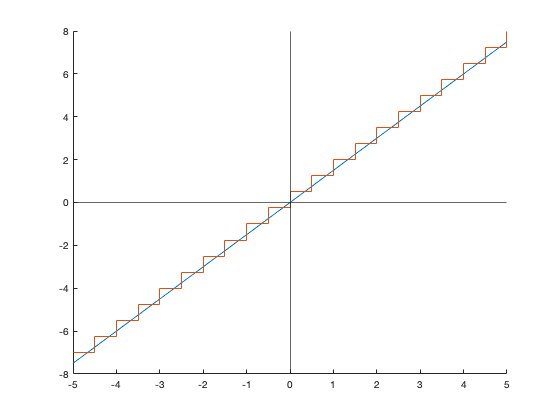Введение

Если открыть спецификацию на любой rtl-sdr приемник, то можно увидеть следующую характеристику: АЦП - 8 бит. Почему эта характеристика важна? Почему о ней пишут и что она значит? Я решил разобраться и провёл небольшое расследование.

SQNR

АЦП преобразует сигнал из аналогового вида в цифровой. Это преобразование по своей сути всегда неточное. Дело в том, что аналоговый сигнал непрерывный, а цифровой - набор отсчетов. Процесс преобразования сигнала называется квантированием. При этом часть информации теряется, а значит, в терминах обработки сигнала появляется шум. Этот шум называется шумом квантования. Обычно правда используют другой параметр - отношение сигнала к шуму квантирования (SQNR).

$$ SQNR = 20\log_{10}(\dfrac{V_{rms}}{V_{e}}) $$

где \(V_{rms}\) - это средне квадратичное сигнала (синусоиды), \(V_{e}\) - это средне квадратичное ошибки квантирования.

В общем случае среднее квадратичное (RMS) это:

$$ V_{rms} = {\sqrt{{\dfrac{V_1^2 + V_2^2 … V_N^2 }{N}}}} $$

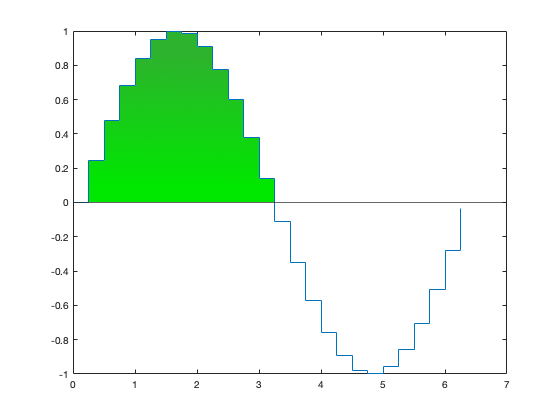
Средне-квадратичные синусоиды лучше представить графически:

Поскольку верхняя часть равна нижней, то значение RMS не зависит от того, как много половинок проинтегрировано. Поэтому достаточно проинтегрировать только зеленую часть. RMS синусоиды вычисляются следующим образом:

$$ V_{rms} = {\sqrt{\dfrac{1}{T}\int_{0}^{T}x^2(t)dt}} $$

Где \(x^2(t)\) - это уравнение синусоиды.

Уравнение в данном случае лучше записать в следующем виде:

$$ \begin{align} x(t) = x_{peak}sin(t\dfrac{2\pi}{T}), \newline V_{rms} = {\sqrt{\dfrac{x_{peak}^2}{T}\int_{0}^{T}\dfrac{1}{2}(1-cos(2\dfrac{2\pi}{T}t)dt}} \newline = {\sqrt{\dfrac{x_{peak}^2}{2T}(T - sin(\dfrac{4\pi}{T}t)\dfrac{T}{4\pi}\Big|_0^T)}} \newline = {\sqrt{\dfrac{x_{peak}^2}{2T}(T - \dfrac{T}{4\pi}(sin(4\pi) - sin(0))}} \newline = \dfrac{x_{peak}}{\sqrt{2}} \end{align} $$

Теперь нужно найти \(x_{peak}\). Его можно выразить следующим образом:

$$ x_{peak} = \dfrac{q2^n}{2} $$

Где n - это количество битов АЦП, q - разница уровня между двумя соседними битами. Если подставить в формулу, то получится следующее:

$$ V_{rms} = \dfrac{q2^n}{2\sqrt{2}} $$

Теперь необходимо найти \(V_{e}\). Как доказал Bennett, ошибка описывается пилообразной волной. Она получается из следующего графика:

Где синий график - это аналоговый сигнал, а красный - это цифровой.

Если вычесть один из другого, то как раз получится пилообразная волна:

Этот график описывается формулой:

$$ e(t) = st, \dfrac{-q}{2s} < t < \dfrac{q}{2s} $$

Для линейного графика RMS будет выглядеть следующим образом:

$$ \begin{align} V_{e} = \sqrt{\dfrac{s}{q}\int_{-q/2s}^{q/2s}(st)^2dt} \newline = \dfrac{q}{\sqrt{12}} \end{align} $$

Теперь если подставить все значения в формулу:

$$ \begin{align} SQNR = 20\log_{10}(\dfrac{V_{rms}}{V_{e}}) \newline = 20\log_{10}(\dfrac{q2^n / 2\sqrt{2}}{q / \sqrt{12}}) \newline = 20\log_{10}(2^n\sqrt{\dfrac{3}{2}}) \end{align} $$

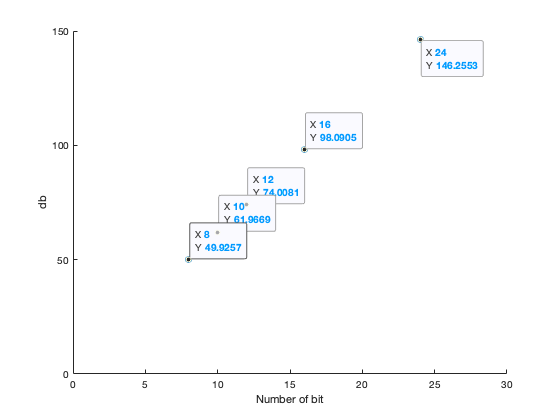
После этого можно построить график зависимости SQNR от числа битов:

Выводы

Из этого графика можно сделать интересные выводы. Например, динамический диапазон rtl-sdr не может быть больше 50db. Это очень важно применительно к измерению качества фильтров. Например, большинство FM фильтров имеют коэффициент ослабления около 60db. А это значит что с помощью rtl-sdr нельзя будет измерить такие фильтры.